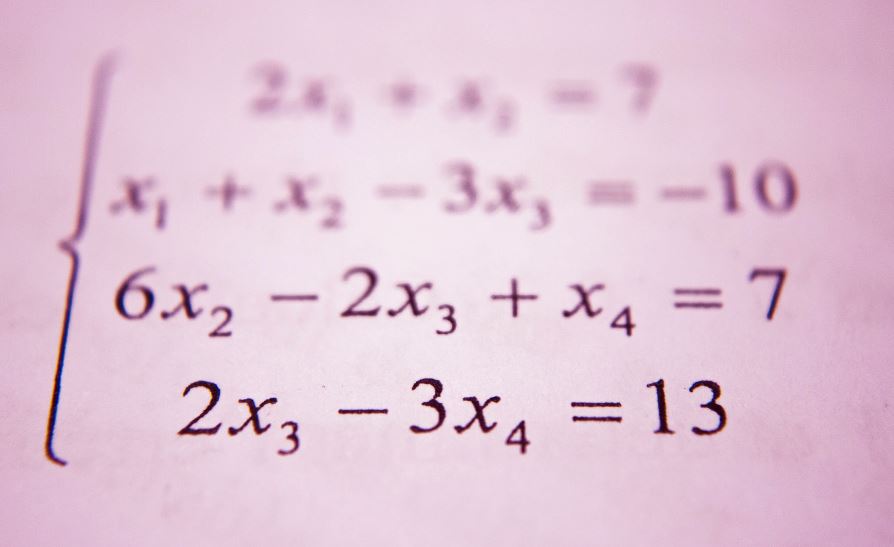There are different types of matrices in the world of mathematics and broadly they are categorized based on the number of elements, order, number of rows, number of columns, and several other kinds of things. With the utilization of different kinds of conditions, different types of matrices can be categorized and everything will be based upon different definitions and examples.
Following are some of the basic types of matrices in mathematics:
- Row matrix: This will be the matrix that will have only one row and will be known as the row matrix. The order of this particular matrix will be one into N.
- Column matrix: This will be the matrix that will have only one column and is known as the column matrix. The order of this particular matrix will be M into one
- Zero or null matrix: This will be the matrix in which every element of the matrix will be zero and has been denoted by zero only. It can be of any order and every element of the matrix will be zero.
- Singleton matrix: This will be the matrix that will have only one single element and is known as the single term matrix.
- Horizontal matrix: Any kind of matrix which will be of the order of M into N will be the horizontal matrix. In this particular case, N will always be greater than M
- Vertical matrix: Every matrix which will be of the order of M into N will be the vertical matrix and in this particular case and will always be greater than N.
- Square matrix: If the number of rows and number of columns in the matrix is equal then it will be known as the square matrix.
- Diagonal matrix: If all the elements except the principal diagonal are into a Square matrix or zero then it will be known as the diagonal matrix. It is very much important for the kids to be clear that the diagonal matrix will always be a Square matrix and the diagonal elements will be characterised by a general form which will make sure that this particular matrix will only be having one single diagonal.
- Scalar matrix: If every element of the diagonal of a diagonal matrix is equal then it will be known as the scalar matrix.
- Unit matrix or identity matrix: If all the elements of a principal diagonal into the diagonal matrix are one then it will be known as the unit matrix. Every identity matrix will be the scalar matrix and every scalar matrix will be the diagonal matrix and every diagonal entry will be the square matrix.
- Equal matrices: These will be the matrices that are very much equal in terms of their elements and the condition will be in the form of the equality of matrices.
- Triangular matrix: This particular Square matrix is known as the triangular matrix because the elements above or below the principle triangle will be zero. The upper triangular matrix will be the one in which the upper triangle will be of normal numbers and the lower triangle will be 0. On the other hand, the lower triangular matrix will be the one in which the upper triangle will be zero and the lower triangular will have elements.
- Singular matrix and the nonsingular matrix: A particular matrix is always known to be the singular matrix if the determinant will be equal to 0 if the nonsingular matrix will be the one if the determinant is not equal to 0.
It is very much vital for the kids to be clear about the basic classification of the matrices and apart from this they also need to be clear about the matrix multiplication rules and conditions so that they never make any kind of mistake at the time of solving the questions. Hence, adjusting the kids on platforms like Cuemath is the best way of ensuring that they can have a good command over the entire process of matrices very easily.